Posit 浮点数格式：IEEE 754 的绝妙替代
Table of Contents
IEEE 754 [2019] 是用位数有限的计算机数据格式表示范围无限的实数的通用标准，它定义了：
- 算术格式：二进制和十进制浮点数据集，包括有限数（包括有符号的零和次正态数）、无限数和特殊的 “非数字 “值（NaN）。
- 交换格式：编码（比特字符串），可用于以有效和紧凑的形式交换浮点数据。
- 舍入规则：在算术和转换过程中对数字进行舍入时需要满足的属性。
- 算术操作：算术格式的算术和其他操作（如三角函数）。
- 异常处理：特殊情况时的行为（如除以零、溢出等）。
自1985年 IEEE 754 标准发布以来，它已经是计算机中表示实数的标准格式，被各种软硬件厂商广泛使用。但是，IEEE 754 标准的定义的浮点数有许多令人不满的地方，这里介绍John Leroy Gustafson博士提出的 posit 格式。
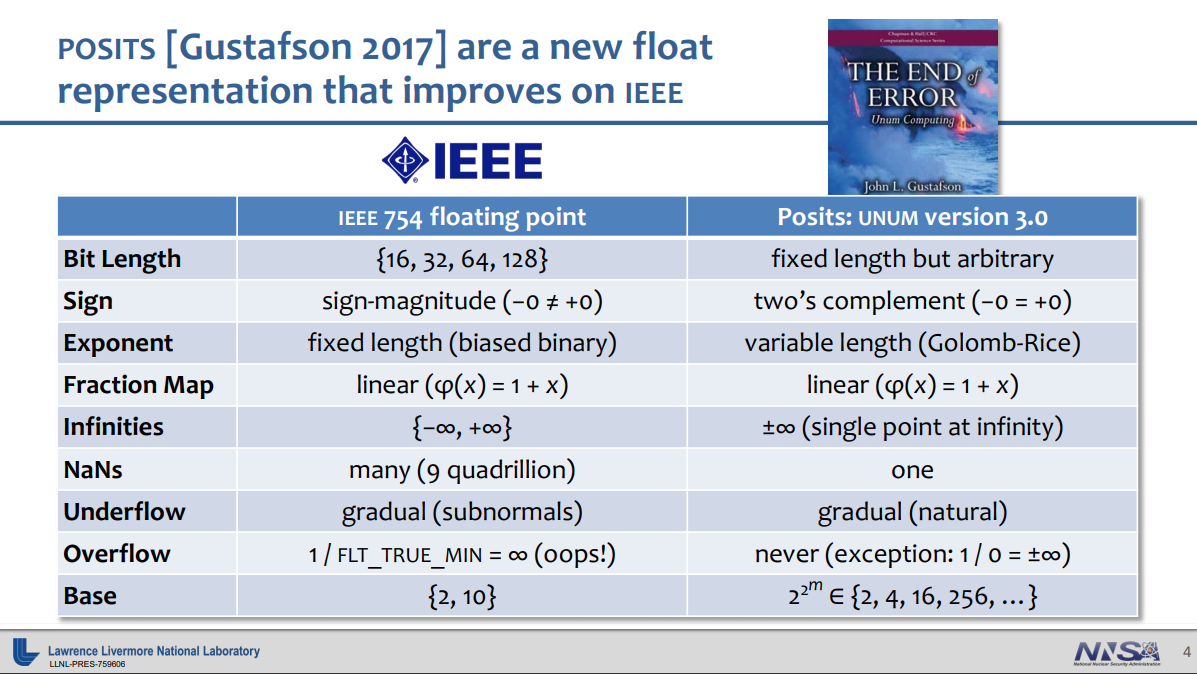
回顾 IEEE 754 格式
编码格式
IEEE 754 把浮点数分成三个部分：符号位(sign)、指数位(exponent)和尾数位(mantissa)。
符号位用来表示正负，指数位用来表示指数，尾数位用来表示尾数。IEEE 754 标准定义了四种浮点数格式：单精度（32 位）、双精度（64 位）、扩展精度（80 位）和四倍精度（128 位）。这四种格式的区别在于指数位和尾数位的位数不同.
于是从浮点数的二进制表示到浮点数数值的计算方法：
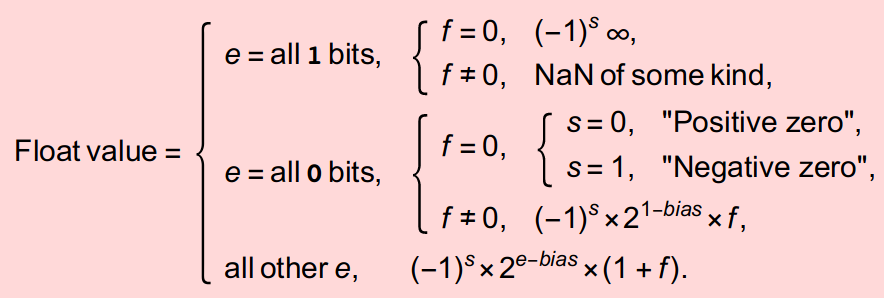各格式浮点数各部分的位数如下：
| bits of S | bits of E | bits of M | |
|---|---|---|---|
| bfloat16 | 1 | 8 | 7 |
| half (binary16) | 1 | 5 | 10 |
| single float (binary32) | 1 | 8 | 23 |
| double (binary64) | 1 | 11 | 52 |
| Quadruple (binary128) | 1 | 15 | 112 |
| Octuple (binary256) | 1 | 19 | 236 |
对于 bfloat16, \(bias(bfloat16) = 2^{8 - 1} -1 = 127\)
对于 half, \(bias = 2^{5-1} -1 = 15\)
对于 float, \(bias = 2^{8 - 1} -1 = 127\)
对于 double, \(bias = 2^{11 - 1} -1 = 1023\)
对于 quadruple, \(bias = 2^{15 - 1} -1 = 16383\)
对于 octuple, \(bias = 2^{19 - 1} -1 = 262143\)
例子
单精度浮点数
对于一个单精度浮点数，二进制表示为 0b0-10000000-10010010000111111011011 ，连字符用于区分它的各部分。
- 符号： \(s = 0\)
- 指数： \(e = (10000000)_{2} = (128)_{10}\)
- 尾数： \(1 + f = (1.10010010000111111011011)_{2}\)
以2为基数计算数值 : \((-1)^{0} \times 10^{10000000 - 01111111} \times 1.10010010000111111011011 \)
以10为基数计算数值 : \((-1)^{0} \times 2^{128 - 127} \times (1 + 1 \times \frac{1}{2^{1}} + 0 \times \frac{1}{2^{2}} + 0 \times \frac{1}{2^{3}} + 1 \times \frac{1}{2^{4}} + \dots )= 3.1415927410125732421875×10^{0} \)
这就是在代码中写 float pi = 3.141592653 ，最终这个 pi 会被舍入的结果。
双精度浮点数
假设一个 double 的二进制表示为:
0b1-00000000000-0000000000000000000000000000000000000000000000000000000000000001
符号位全为0，尾数位不全为0，这是个非规格化浮点数，它的数值等于多少？
- 符号： \(s = 0\)
- 指数： \(e = (00000000000)_{2} = (0)_{10}\)
- 尾数： \(f = (0.0000000000000000000000000000000000000000000000000000000000000001)_{2}\)
以2为基数计算数值为:
\((-1)^{0} \times 2^{1 - 1023} \times (0 + 0 \times \frac{1}{2^{1}} + 0 \times \frac{1}{2^{2}} + 0 \times \frac{1}{2^{3}} + 0 \times \frac{1}{2^{4}} + \dots )=(-1) \times 2^{-1022} \times 2^{-52} = 2^{-1074} \approx 4.94065645841246544177 \times 10 ^{-324} \)
bfloat16 浮点数
一个 bfloat16 的二进制表示为 0b0-11111111-0000000
很显然，这表示 bfloat16 的 ~+ ~ 。
IEEE 754 的一些问题/特性
表示0附近的小数值时
小数字的大尺寸。IEEE 754标准为单精度和双精度数值表示定义了两种特定的格式，分别使用32位和64位。在这些格式中，有限的数值范围内的数字计算可能在很大程度上是低效的。例如，计算[-1, 1]范围内的数值的点乘，只需要用这两种格式表示的所有可能的数字中的一小部分。
破坏代数规则
在计算过程中，浮点格式可能会破坏代数规则。例如，浮点加法并不总是满足结合律的。表达式 (x+y)+z 的结果是 1 ，其中浮点值为 x=1e30，y=-1e30，z=1,使用相同的值， x+(y+z) 的结果是0。
不同的表示产生不一致的结果
考虑两个向量 Q=(3.2e7, 1, -1, 8.0e7) 和 W=(4.0e7, 1, -1, -1.6e7) 。
点积 Q.W 在单精度中等于0，双精度中等于1,而正确的答案是2。使用 IEEE 754，需要80个中间位才能产生双精度格式的正确答案。
把浮点异常编码在浮点数中，浪费大量位模式并且增加了处理器的复杂性
-0 的存在有意义吗
除了给程序员（包括软件程序员还是硬件程序员）带来麻烦之外。
大量的位模式用来表示 NaN
对于三个部分为 1 8 23 的 float来说，它的NaN有 \(2^{24} -2\)个。NaN本来是表示运算中出现的错误或者特殊值，这么多NaN不如把它们都用来表示正常的数值。
除法很难
看一下我们 map500 ISA 里做除法的几个指令就懂了。
硬件复杂的设计和验证
要写处理舍入、浮点异常、NaN、正负值、尾数对齐等必要的组件。要处理各种corner case，例如各种NaN参与运算，+0和-0参与运算，无穷大参与运算等等。验证浮点设计也很难。Pentium 1994 年的 bug就是因为浮点数的处理。
Posit 浮点数格式
posit 格式包括一个必须的符号位，必须的一个或多个 regime 位，多个可选的指数位，和多个可选的尾数位。
在符号位之后，regime 包括一个0或1的序列 rr...r ，由一个相反的位（r̄）结束。指数和尾数的位数也是动态的。一个数只在必要时包括指数和尾数。
m为regime位（琥珀色）中相同的位数。如果第一个比特是零，零的数量（m）代表一个负值（-m）。否则，1的数量减去1（m-1）代表一个正值（m-1）。把这个值记作k.- \(useed = 2^{2^{es}}\) ，其中
es为指数位的位数。
那么一个 posit 数从它的二进制表示到数值的转换公式为：
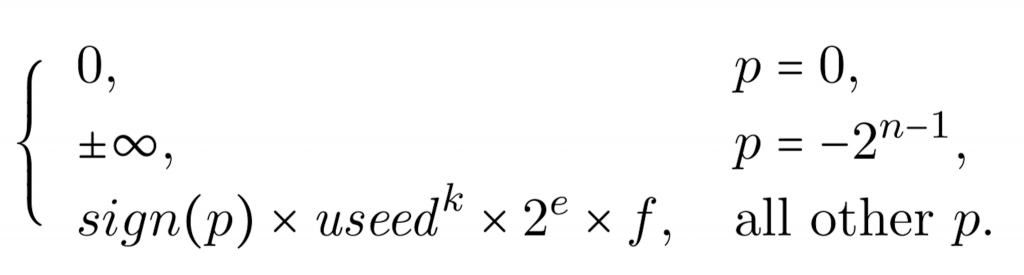
假设我们有一个 4 位的 posit 格式，其中 1 位符号位，2 位指数位，2 位尾数位。那么，这些 posit 数为：
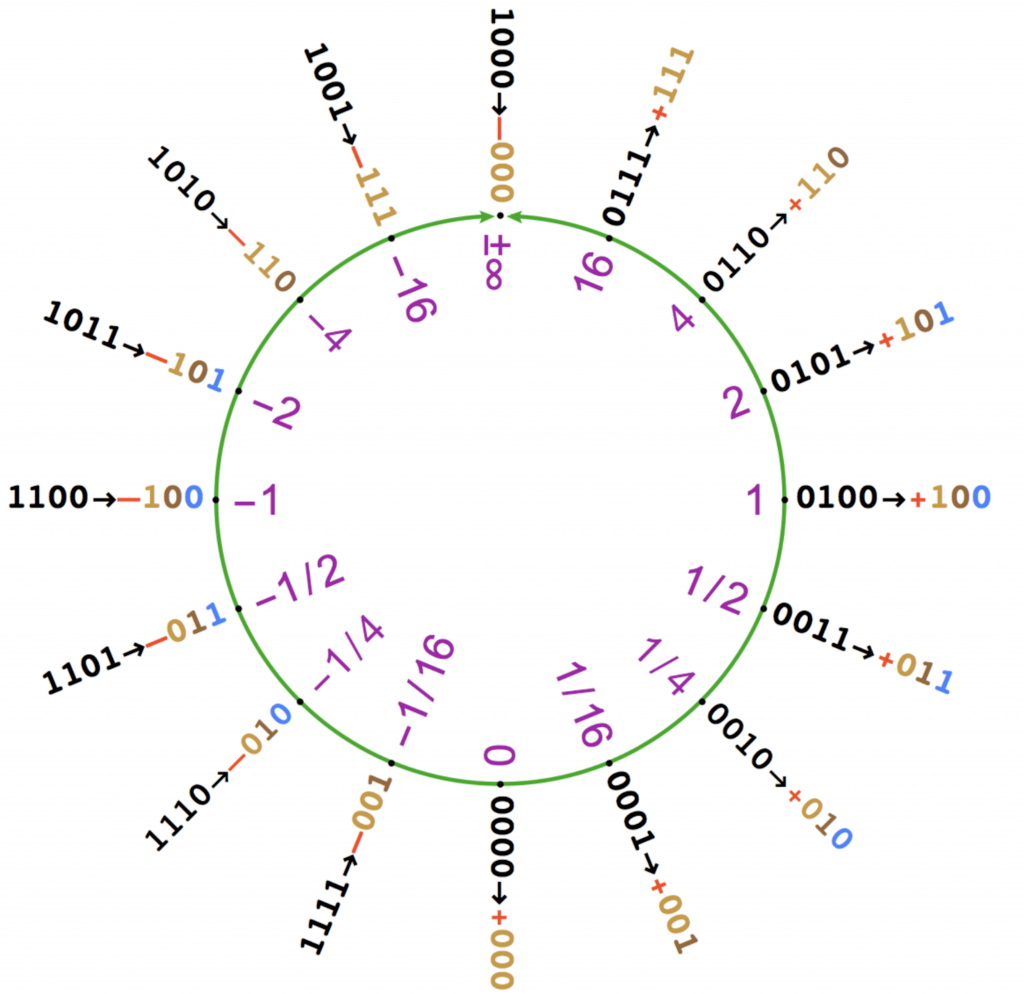
可以看到，在一种具体的 posit 格式下，实数0只有一种表示：所有位为0.
第一个位为1，其余位为0的数是一个特殊值，被称为 NaR （Not a Real number）。
规定了一个具体的 posit 格式（总位数，regime 位数， es）后，这个唯一的特殊值也就确定了。
例子
对于一个 16 位的 posit 格式，其中 1 位符号位，3 位指数位(es = 3)，8 位尾数位，那么位模式 0b0-0001-101-11011101 表示：
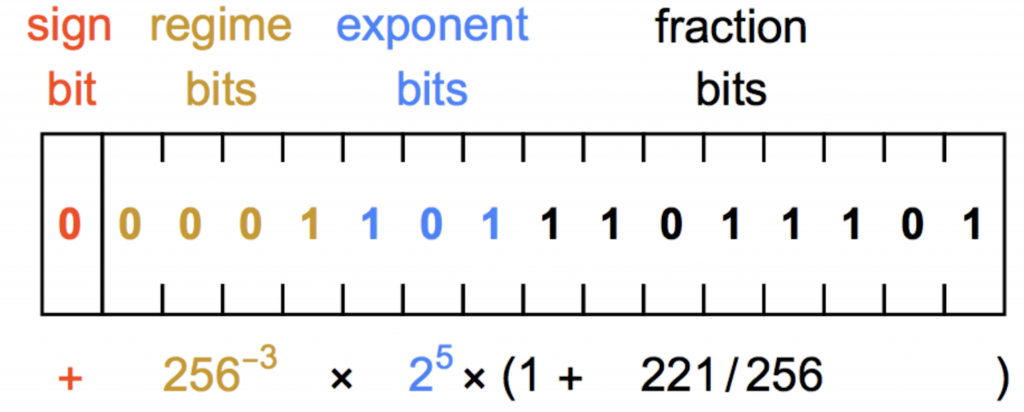
- \(s = 0\)
- \(es = 3, useed = 2^{2^{es}} = 256\)
- \(k = -3\)
- \(1 + f = 1 + (11011101)_{2} = 1 + \frac{221}{256}\)
数值为：\((-1)^{s} \times useed^{k} \times (1 + \frac{221}{256}) = 256^{-3} \times( {1+\frac{221}{256}})\)
Quire 浮点数格式
Quire 相当于几个 posit 浮点数的折叠，可以用来实现高精度的融合运算，具体参考 posit 标准： https://posithub.org/docs/posit_standard-2.pdf . [Gustafson and Yonemoto 2017]
Posit 与 Quire 的优势
值有唯一表示
在posit格式中，如果a和b相等， f（a） 总是等于 f（b） ，其中f是一个函数。在IEEE 754中，正零和负零的倒数分别为 \(+\infty\) 、\(-\infty\)。此外，负零等于正零。这意味着\( +\infty = -\infty\)，这是不正确的。
在IEEE 754比较中 \(a = b\) ，如果a或b其中有一个是NaN，其结果总是假的，即使a和b有相同的位表示。而在posit中，如果a和b使用相同的位模式，它们是相等的；否则，它们是不相等的。此外，在不同的硬件系统上，算术运算的结果将是相同的。在前面的Q.W的例子中，posit只需要24位就可以产生正确的结果。
不需要特殊机制实现逐渐下溢
当一个操作的确切结果为非零但小于最小的规格化数字时，IEEE 754面临一个下溢问题。这个问题可以通过四舍五入来缓解。然而，这可能会导致一个不正常的数字。也就是IEEE 754在处理比较小的数时，符号位因此，一些尾数数字被转移到指数上以表示更小的数字。这就是所谓的渐进下溢。
处理逐渐下溢很复杂，一些符合 IEEE 754 标准的处理器用软件支持而不是硬件实现。posit 不会遇到这个问题，因为它支持可变精度，小指数的数字比大指数的数字表示得更准确。
保持代数规则
posit 保持加法结合律。
在具有不同大小的多个 posit 格式中计算数值，可以保证产生相同的数值。
异常处理
posit 没有 NaN ，只有一个单一的 NaR, 它即表示也 NaN 也表示无穷大。
总的来说，posit数字的计算比IEEE 754更简单。
发生异常的情况下（比如除以0），中断处理程序应向应用程序报告错误及其原因而不是让程序把错误编码在计算结果中。
与IEEE 754的兼容性
posit 标准里定义了与 IEEE 754 的转换规则。理论上，硬件只要实现了这些转换单元就可以用 posit 格式来替换 IEEE 754 格式。
业界目前的采用
目前实现 posit 的硬件屈指可数。
John Leroy Gustafson的公司
他们的 posit 处理单元将会集成在在 amd 、intel 以后的计算卡里。
香山处理器
我业余时间在用 chisel 写的硬件 posit 库（https://github.com/VitalyAnkh/hardposit-chisel3)之上给香山处理器的浮点模块添加了 posit 支持，尚未完成，预计还需要半个月，做完后会做一个benchmark，比较单纯的posit处理和加了posit 和 IEEE 754兼容层的性能.
PERCIVAL
[Mallasén et al. 2022] 这篇文章的研究者在一个 RISC-V 处理器上实现了 posit 的硬件支持，显示出30~40%的性能提升。